Composed stochastic proof : joint distribution monad as dependent type (part 3 of 4)

composed stochastic proofs - motivation

I posted some background links and concepts on Reddit r/DepdendentTypes
Dependent Types for Giry probability monads, e.g. Kantorovich / Wasserstein (+ followup comment)

In this post, we begin tackling the kinds of distributions needed for our
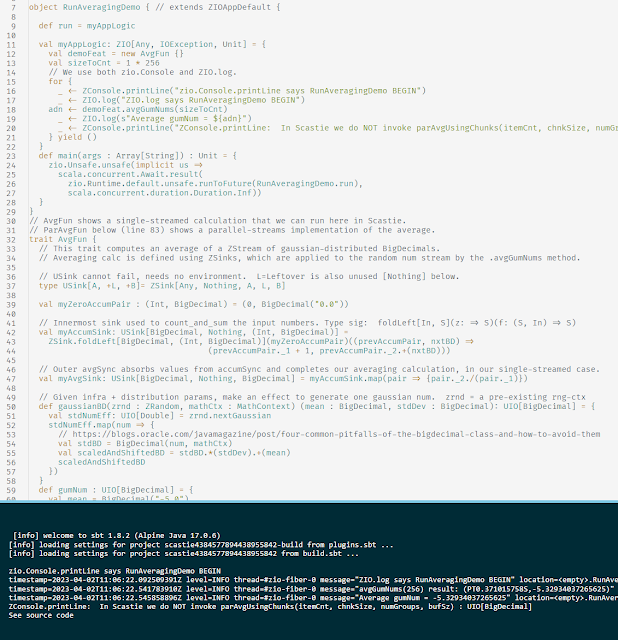
Asset Allocation Example.

joint distribution monad as dependent type

We define our strong typed stochastic computing structure in these 3 stages

1) Mathematically, in informal human-readable equations and type descriptions
     (formally encoded and exposed as visible API in 3 below, using infra from 2)

2) As functional abstractions, using the kantorovich monad formulation
     (formally encoded as submerged infrastructure, used by 3 below)

3) As a formal dependent-typed API usable from suitably strong-typed environments such as

  • Lean, F*
  • Idris
  • Agda, Coq, Isabelle, HOL, MMT
  • Scala 3 (Dotty)

Restating the WHAT:  The software types defined formally in 3 are refinements of the informal types from 1, relying on an infrastructure of types and proofs for the kantorovich monad from 2.  
Restating the HOW:    Given a proof environment 3 containing sufficient elements from 2, then the API types 1 may be implemented faithfully, using dependent type engineering principles.

Our workhorse example is a robust platform-neutral distribution monad, for a finite-dimensional vector space of possible events.   

  • One outcome/sample is one vector. 
  • The distribution is presumed to be Lebesque integrable.  (This presumption is enforced by our monad types).
  • Primarily we are interested in cases with bounded support (where the coordinates of the sample vector are bounded).

Users see this distribution as a robust joint distribution over the dimensions of the event space.   
A common example uses events in a convex subspace of euclidean R^N == The ordinary N
dimensional real vector space, with euclidean norm, which is a (Banach) complete metric space. 

Then one sample X is one N-vector of real components {X_n} == (X_1, X_2, ... X_N), where each of the X_n is an in-bounds real number.  In a simple example, the bounds are separable as N pairs of constraint inequalities:
   {B_n_MIN <= X_n <=  B_n_MAX}    

The probability of an outcome X is governed by D_X, the distribution of X, which to a user is a
joint probability distribution over the components {X_n}.   

D_X is usable both analytically and numerically:

  • D_X is composable using monadic laws, to produce conditionals, marginals, expectations, moments
  • D_X may be used as a source of samples, for visualization and monte carlo methods
  • D_X may be projected into a reduced resolution sample space.
    • For example, a continuous distribution over the X_n may be projected into a coarse discrete distribution, which is still a joint distribution.
      • Imagine a histogram with M bins for each X_n :  {B_n_m}
      • Each of the bin-sets {B_n_*} is selected independently from the others
      • Total bin-level parameters required:  N * M
      • Reduced sample space is just Z_M ^ N, i.e. an N vector of integers between 1 and M.  
      • Reduced event space has M ^ N elements.   
      • Each of these possible events may be assigned a discrete probability, from either a computable function or a literal dataset (e.g. using frequentist statistics).  
      • Each discrete probability may be reliably assigned as a rational number, enabling proof that the distribution function is properly normalized ; i.e. it sums to 1.
      • This finite description of a finite distribution over R^N is computationally tractable using integer methods.  
        • Demonstrate for small euclidean event-space
        • Demonstrate for larger spaces and different event-space norms
      • However, this finite description has fewer analytic guarantees than the original continuous distribution.
      • M may be increased / decreased to trade resolution for computational workload.
    • Both the continuous and discrete distributions are composable monads.

This flexible applicability of D_X allows us to design and perform useful, sharable
experiments with minimal attention (initially) to platform considerations.   
D_X is a verifiable stochastic model, not a platform-dependent piece of implementation code.
When a particular distribution is proven useful, then it may be promoted into use in high-scale computing environments (potentially with our proof system compiled into the runtime).  

Domain types based on probability monads is the fourth and final article in this series, addressing some aspects of implementation, for cases with low event-space dimensions.

Resources for understanding the Kantorovich monad are listed and discussed in this Reddit thread:

More reference pages:


Popular posts from this blog

Overview of AxLam model : Nouns, Types, Morphisms

2023-Feb-03 picking up from tweet thread of 220909  AxLam model: Noun (space), Type (paint), Morphism (arrow) AxLam is for writing models using [concepts, types, and morphisms].  Our concepts may be in the form of some data, or less specifically as things we choose to name or refer to in a model.  Over this concept space, we use types and morphisms to define an adjustable descriptive model that directs and regulates processing of the concept data (or other manifestation).  Alternatively and  more approachably we may write in terms of [nouns,  formal classes, and mappings], and this framing is mostly equivalent for informal purposes. Nouns / Concepts / Terms / Data Nouns (i.e. concepts) describe anything we wish to refer to, and need not be explicit or named.  We think of nouns as the space of things we might try to describe, name or refer to.  "Terms" in a type-theoretic sense are nouns.  Real things in the human world that someone cares abo...
Read more

Streaming analytics in Scala using ZIO and Apache DataSketches (part 1)

Image
First let's look at a trivial example of streaming analytics using ZIO Streams 2.0.9 (on Scala 2.13). https://scastie.scala-lang.org/6AHfPh02S6m0k7aN6bkacA When run, this Scastie just averages some random numbers (gaussian) in a single input stream.  That code is in the trait AvgFun . But we also see a trait called ParAvgFun with the code for rather painless parallel  implementation, using ZIO chunks, via ZStream's  grouped , zipWithIndex , and groupByKey .  Across these two traits, the clean reusability of ZSinks in different pipelines shows a nice design win for the ZIO Streams API.   The code in  ParAvgFun.parAvgUsingChunks  demonstrates a terse and reasonably efficient design for accumulating results using parallel ZStreams (within a single process).  It is applicable to  simple cases where the stream elements are lightweight and similar, and the underlying operations are uniformly easy (like summing numbers).  When inste...
Read more

AxioMagic under Spark on cloud (AWS, Azure, ...)

AxioMagic under Spark on ${ cloud  } AxioMagic relies on functional composition over immutable inputs, thus matching modern evaluation frameworks like Apache Spark, which defines a structured approach to managing data contexts of functional evaluation over data frames.  Spark embodies a refinement of both  ETL and MapReduce methodology.  State machines like Spark require computation and storage resources which may come from any cluster, but today are commonly provided from cloud environments, yielding high volume functional computation at predictable usage-based costs.  We especially value Spark for open scientific dataset analysis, where it is common to work with large data files in interchange formats. Essential features of Spark distributed evaluation Spark assembles batch pipelines to pump datasets of structured records through functional tasks (which may  invoke side-effects, with all necessary stipulations).  This pipeline serves to evaluate...
Read more