Streaming analytics in Scala using ZIO and Apache DataSketches (part 1)
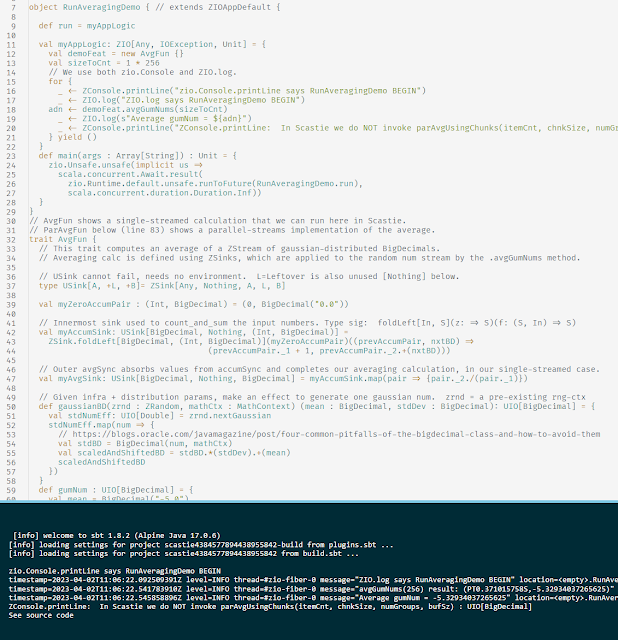
First let's look at a trivial example of streaming analytics using ZIO Streams 2.0.9 (on Scala 2.13). https://scastie.scala-lang.org/6AHfPh02S6m0k7aN6bkacA When run, this Scastie just averages some random numbers (gaussian) in a single input stream. That code is in the trait AvgFun . But we also see a trait called ParAvgFun with the code for rather painless parallel implementation, using ZIO chunks, via ZStream's grouped , zipWithIndex , and groupByKey . Across these two traits, the clean reusability of ZSinks in different pipelines shows a nice design win for the ZIO Streams API. The code in ParAvgFun.parAvgUsingChunks demonstrates a terse and reasonably efficient design for accumulating results using parallel ZStreams (within a single process). It is applicable to simple cases where the stream elements are lightweight and similar, and the underlying operations are uniformly easy (like summing numbers). When inste...
