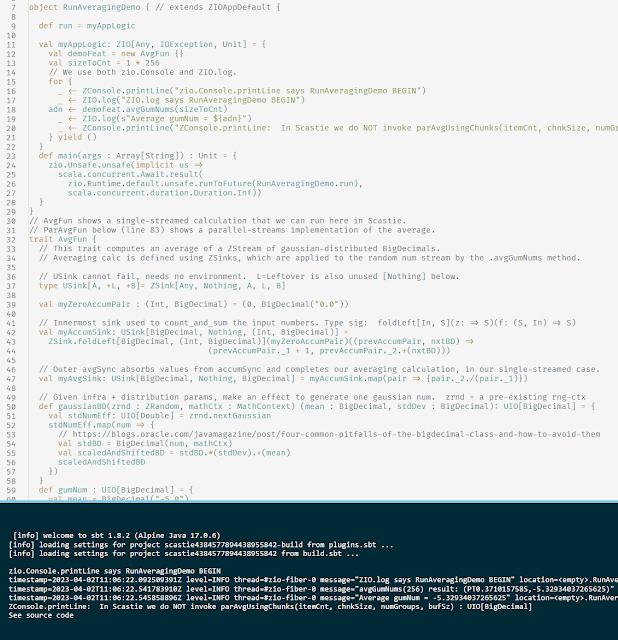
AxLam Example : Questions about Triangles

Consider the humble, mighty triangle:  a connected shape with 3 vertices, 3 sides, and 3 angles.  We will experiment with AxLam models for describing and computing with triangles individually and in groups, at several levels of mathematical rigor.  On this road we touch briefly on some fundamental aspects of mathematics and information, while staying intuitively grounded in the triangle simplex.  

In a computer-assisted modeling paradigm, it is natural to proceed constructively.
An intuitive way to start modeling triangles is using the lengths of the 3 sides of the triangle.
In any programming or data language, we might quickly write down an ADT, record or class containing  three numeric sides, looking something like:

class  TriangleSidesRecord (sideA : Number, sideB : Number, sideC : Number)

This structure is sufficient to begin computing with Triangles.  However, when we examine the semantics of this simple record structure, we quickly find many issues.  Phrased as questions, each of these issues implies a kind of mathematical analysis we are subjecting our triangle model to.

1. How do we ensure that a triangle's side lengths obey the triangle inequality?
2. How do we know when two triangles are congruent or similar?
3. How can we work with the space of all unique triangles, up to congruence or similarity?
4. How does our sides-based model relate to a an alternate model describing a triangle in terms of its angles?
5. How can we work with subspaces of triangles having a symmetry property (isosceles, equilateral) or a 90-degree right angle, or other conditions we express in terms of the sides or angles?
6. When working with a subspace of triangles, when and how may we compute its cardinality?
7. When and how may we enumerate all elements of a subspace, possibly in some helpful order? 
8. Under what conditions can we compute the perimeter and area of a triangle, and how exact is this computation?
9. What relationships hold when a triangle is divided into sub-triangles?
10. THE BIG ONE:   How does the nature of the Number type of the sides (or angles) influence our thinking about these issues? 
11. Metric topology perspective:  What are some natural forms of distance we might compute between two triangles?
12. Statistical perspective:  Given a (possibly infinite) set of triangles, a property of interest (e.g. perimeter or area), and a set of value ranges (called "bins") for the property, how may we construct a histogram? That is, how can we determine the fraction of triangles that fall into each bin?
13. Algebraic topology perspective:  Recognizing that triangles are 2-dimensional simplexes, how may we construct higher dimensional simplexes, and complexes? 
14. Suppose some triangles are embedded in a space that is different from the euclidean plane, or potentially not embedded in any space at all.   What information about them is still valid, and what is in doubt?  What assumptions are implied in our notion of "length" and "angle", and what does it mean for a triangle to have "sides" and "vertices"?  
15. Are we able to access information from our triangle-based datasets in an appropriately lazy manner?
16. How would our  answers to the above impact different engineering applications, such as approximation to a surface using connected triangles?  
17. Which of our answers above contains claims that we can verify using formal proof? 
18. How can different human users of the triangle concept make use of our shared knowledge about triangles, without re-implementing theoretical infrastructure for math and computation? 

The answers to these questions depend on both mathematical knowledge and our modeling approach.
Most software programmers can quickly provide reasonable answers to the first few questions in terms of a familiar system, e.g. using Python or Scala.  However as we move into more subtle and  challenging mathematical questions, the answers come less readily.  In particular, question 10 about the Number type is a trapdoor into the universe of analytical concepts about numbers and computation.  The choices we make about Number will lead us to re-examine the context of our answers to the previous 9 questions.  

To be more concrete:  Suppose that Number means Real number.  This choice aligns our thinking with the common notion of an exact number (a zero-width point on the number line) taught in elementary and secondary schooling, and allows for formal proofs based on known theorems about the real numbers.  However, most ordinary computer programs instead use approximations to real numbers, such as floating point (occupying a non-zero-width interval on the number line).  That floating point representation is efficient and adequate for many programs, but is not suitable for exact models, which we wish to support with proof.  By using the formal concept of an exact Real number, we take on a level of rigor that allows us to construct solid proofs, and use existing proofs governing the Reals.  

Other useful formal types of proof-compatible numbers include Integers, Rationals, and Algebraic numbers.  Consider the triangles whose sides (or angles) are restricted to these different classes of numbers, or sub-classes such as "rational numbers between 0 and 1/2" or "integers between 1 and 5".  Now again our answers to the questions above will change, and interesting new questions may pop out.

This work is an example of what we have called painting type marks like Number, Integer, Rational, Integer[min=1, max=5], to help us organize spaces of nouns, like the space of all unique triangles.