Streaming analytics in Scala using ZIO and Apache DataSketches (part 1)
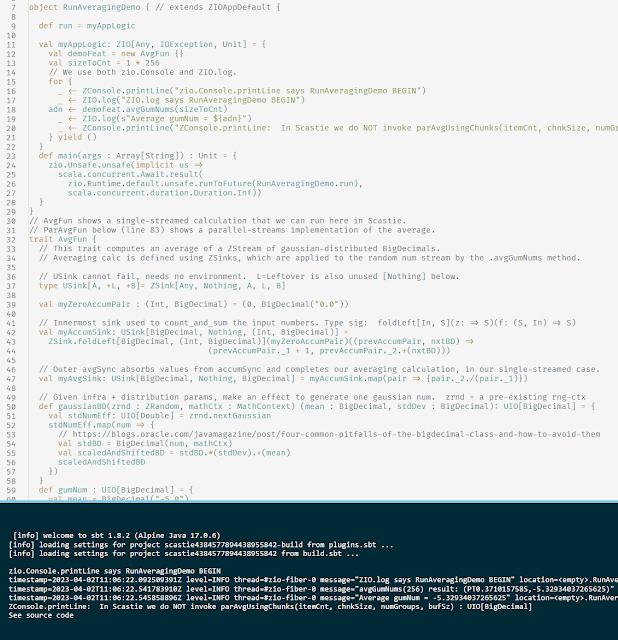
First let's look at a trivial example of streaming analytics using ZIO Streams 2.0.9 (on Scala 2.13). https://scastie.scala-lang.org/6AHfPh02S6m0k7aN6bkacA When run, this Scastie just averages some random numbers (gaussian) in a single input stream. That code is in the trait AvgFun . But we also see a trait called ParAvgFun with the code for rather painless parallel implementation, using ZIO chunks, via ZStream's grouped , zipWithIndex , and groupByKey . Across these two traits, the clean reusability of ZSinks in different pipelines shows a nice design win for the ZIO Streams API. The code in ParAvgFun.parAvgUsingChunks demonstrates a terse and reasonably efficient design for accumulating results using parallel ZStreams (within a single process). It is applicable to simple cases where the stream elements are lightweight and similar, and the underlying operations are uniformly easy (like summing numbers). When instead there is great variability in the cost of proces
